The Fundamental Theorem of Poker

Introduction

In this article I introduce you with the fundamental theorem of poker. You get to know the theorem itself as well as typical misunderstandings regarding its interpretation for practical play.

The theorem

The fundamental Theorem of Poker was introduced by the American poker player and author of numerous poker books David Sklansky in his work The Theory of Poker . In the book the following definition is given:

“Every time you play a hand differently from the way you would have played it if you could see all your opponents‘ cards, they gain; and every time you play your hand the same way you would have played it if you could see all their cards, they lose. Conversely, every time opponents play their hands differently from the way they would have if they could see all your cards, you gain; and every time they play their hands the same way they would have played if they could see all your cards, you lose.”

Essentially, the theorem describes what distinguishes successful play from less successful play. On closer examination it can be divided into the following four statements, the academics would probably say lemmas:

1. Every time you play a hand differently from the way you would have played it if you could see all your opponents‘ cards, they gain.
2. Every time you play your hand the same way you would have played it if you could see all their cards, they lose.
3. Every time opponents play their hands differently from the way they would have if they could see all your cards, you gain.
4. Every time opponents play their hands the same way they would have played if they could see all your cards, you lose.

In his book Sklansky gives several examples by which he examines the applicability of the theorem. At this point I would like to introduce the first example, but I also recommend that you study the book and the other examples mentioned in it.

Example

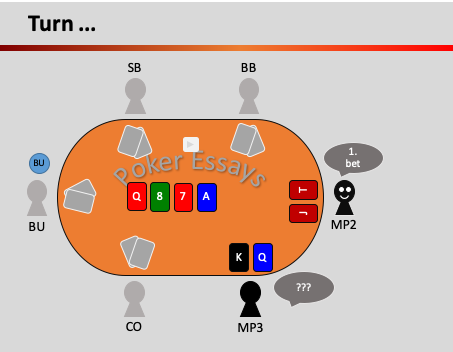
If you try to apply the Fundamental Theorem of Poker, you can make three statements.

• According to the theorem, the correct answer from MP3 would be a raise. This is because if MP3 knew the cards of MP2, she would raise the bet of MP2, so much that the probability of hitting a flush or a straight would be too small for MP2.

If MP3 plays differently than if she knows the cards of MP2, a call or a fold would be possible.

• If MP3 only called, MP2 would have won, because the next card is cheaper than after a raise and still has a chance of winning the pot.
• If MP3 folds, MP2 would have won because he wins the pot with the worse hand.

The example itself may be trivial, but it clearly illustrates the core message of the Fundamental Theorem of Poker. Every time you play a hand differently from the way you would have played it if you could see all your opponents‘ cards, they gain. Every time you play your hand the same way you would have played it if you could see all their cards, they lose.

Misconception about the fundamental theorem of poker

Sklansky provides more examples in his book and also discusses the applicability of the Fundamental Theorem of Poker in multi-way pots. In these, situations can arise where a player would prefer correct play from one of his opponents. This is the case when this results in that player winning more together with the other player at the expense of the opposition in the pot than if all players play as if they knew all other cards. These situations are very special, for the corresponding details I recommend the study of The Theory of Poker .

Sklansky also discusses typical misunderstandings in the context of the Fundamental Theorem of Poker, in particular the understanding of the concept of error or the understanding of correct play.

If you make a mistake in the context of the fundamental theorem of poker, it doesn’t automatically mean that you have objectively played badly. It simply means that you would have played differently if you knew all the cards of your opponents. Take a look at the admittedly very striking example.

MP1 holds a Royal Flush, MP2 a Q-high Straight Flush.

If MP2 knew the cards of MP1, then according to the Fundamental Theorem of Poker she would have to fold to a bet (no matter how small) of MP1 and just check to a check of MP1. Since in the actual game the cards of the other players are unknown, a call or even a raise should be considered, depending on the amount of the MP1 bet, or a bet on a check of MP1.

Summary and prospects

In this article I have introduced you to the Fundamental Theorem of Poker, which is considered by many players to be one of the most important concepts for successful poker play, regardless of what type of poker you play.

The theorem contains the following four statements:

1. Every time you play a hand differently from the way you would have played it if you could see all your opponents‘ cards, they gain.
2. Every time you play your hand the same way you would have played it if you could see all their cards, they lose.
3. Every time opponents play their hands differently from the way they would have if they could see all your cards, you gain.
4. Every time opponents play their hands the same way they would have played if they could see all your cards, you lose.

For a deeper understanding of the underlying concepts, I recommend the study of The Theory of Poker .